Blog
Xem thêm
Nhận khuyến mãi hoàn tiền Go88 cần tuân thủ những điều kiện gì?
Những khuyến mãi đỉnh cao nhất người chơi chỉ có thể nhận được khi tiến hành tham gia tại go88. Khuyến mãi hoàn tiền của nơi đây luôn được những game thủ đánh giá cực kỳ cao. Từ đây người chơi sẽ vô cùng phấn khích khi đến và thưởng thức tại hệ thống. Bài viết dưới đây sẽ giúp cho người chơi những thông tin cần thiết và đầy hữu ích.
Nét thú vị...
Tiết Lộ Mẹo Chơi Bất Bại Trò Chơi Super Mario Tại 789club
789Club từ lâu đã là một cổng game lý tưởng đối với rất đông anh em tham gia chơi cá cược online. Cũng chính vì thế, cổng game đã ra sức mang đến cho anh em những tựa game cá cược hấp dẫn. Trong số đó có tựa game Super Mario – tựa game ăn khách nhất. Hôm nay, anh em hãy cùng chúng tôi đi khám phá sâu hơn nữa về thể loại game cá cược mới...
Phương pháp hiệu quả để săn thưởng khi chơi Xỉu chủ Sunwin
Xỉu chủ một cách đánh lô mới, độc đáo mà phần thưởng lại cực kỳ hấp dẫn khi trúng. Tuy nhiên, độ khó của hình thức cá cược chọn số này khá cao. cược thủ khó lòng chiến thắng được nếu không có kinh nghiệm, cách chơi đúng đắn. Bài viết chia sẻ phương pháp hiệu quả để săn thưởng khi chơi Xỉu chủ Sunwin cho anh em.
Những nét chính về Xỉu chủ...
Tìm hiểu thông tin về giải vô địch bóng đá Đông Nam Á
Giải vô địch bóng đá Đông Nam Á không còn quá xa lạ đối với người hâm mộ bóng đá Việt Nam. Vậy giải đấu này là gì? Bao nhiêu năm tổ chức 1 lần? Và đội tuyển nào giành được nhiều chức vô địch nhất? Mọi thông tin này sẽ được chúng tôi tổng hợp đầy đủ ở bài viết xôi lạc tv. Xem ngay chi tiết nhé!
Giải vô địch bóng...
ggbdichj
levantamtkqn
ngựa hoạt hình
Cartoon funny ponies. Colorful little horses. Magical equine animals. Kids fairy pets. Children carousel decorative isolated elements. Cute stallions with saddles. Galloping mammals. Garish vector set
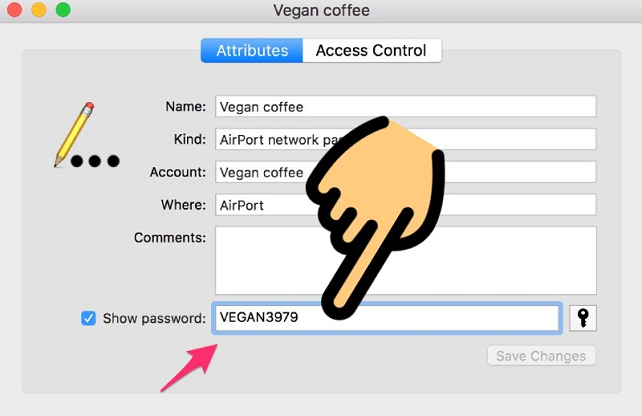
cách xem pass wifi
Cách xem lại mật khẩu Wifi trên điện thoại và máy tính được hướng dẫn chi tiết trong bài viết sau. Cùng theo dõi các bước thực hiện ngay, bạn nhé!
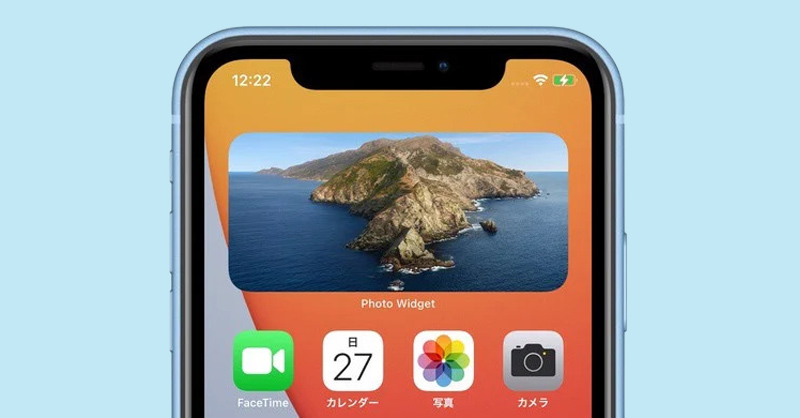
tạo ảnh nổi bật trên iphone
Tìm hiểu về cách thêm ảnh nổi bật trên iPhone iOS 16 để có thể sử dụng trong những trường hợp cần thiết. Từ đó, quá trình sử dụng điện thoại của bạn cũng trở nên thú vị và tiện lợi hơn.
vẽ trang trí đơn giản
Trang trí sổ tay học tập giúp bạn quản lý công việc học tập hiệu quả và cải thiện khả năng tập trung. Xem ngay cách trang trí sổ tay học tập sáng tạo.
thời tươi đẹp của chúng ta
Câu chuyện về gia đình ông bà Song Young Dal có bốn người con với... ba cuộc ly hôn trong bộ phim 'Thời tươi đẹp của chúng ta' đang mở ra những tình huống bất ngờ, hài hước nhẹ nhàng.
Copyright © 2023 All Rights Reserved.