Khám phá ngay quy tắc lũy thừa dễ dàng với các công thức vô cùng đơn giản
Quy tắc lũy thừa là một trong những kiến thức quan trọng của môn Toán học, giúp bạn hiểu và giải quyết các bài toán liên quan đến số mũ. Bài viết này sẽ cung cấp các công thức lũy thừa chi tiết, dễ hiểu và có ví dụ minh họa để bạn có thể áp dụng một cách hiệu quả.
Quy tắc lũy thừa là gì?
Quy tắc lũy thừa là những quy tắc cơ bản trong toán học giúp chúng ta tính toán và rút gọn các biểu thức có chứa lũy thừa. Lũy thừa là một phép toán, trong đó một số hoặc một biểu thức được nhân với chính nó một số lần nhất định. Quy tắc lũy thừa bao gồm những nguyên tắc cơ bản về cách thực hiện các phép toán như nhân, chia, và lũy thừa của một lũy thừa. Dưới đây là các quy tắc lũy thừa chi tiết.
Quy tắc nhân hai lũy thừa cùng cơ số
Nếu hai lũy thừa có cùng cơ số, ta nhân chúng bằng cách cộng các số mũ lại. Công thức tổng quát:
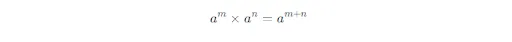
Trong đó:
- aaa là cơ số (số bị lũy thừa).
- mmm và nnn là các số mũ.
Quy tắc chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa có cùng cơ số, ta lấy số mũ của lũy thừa thứ nhất trừ đi số mũ của lũy thừa thứ hai. Công thức tổng quát:
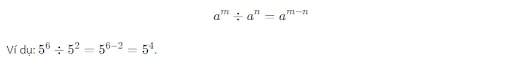
Quy tắc lũy thừa của một lũy thừa
Khi nâng một lũy thừa lên một số mũ khác, ta nhân các số mũ lại với nhau. Công thức tổng quát:
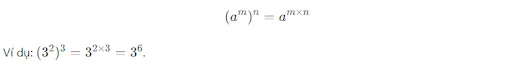
Quy tắc lũy thừa của một tích
Khi có một tích của các số và muốn nâng tích đó lên một lũy thừa, ta có thể nâng từng số trong tích lên lũy thừa đó. Công thức tổng quát:
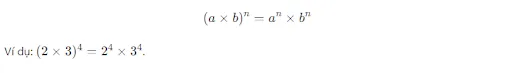
Quy tắc lũy thừa của một thương
Khi có một thương của các số và muốn nâng thương đó lên một lũy thừa, ta có thể nâng từng số trong thương lên lũy thừa đó. Công thức tổng quát:
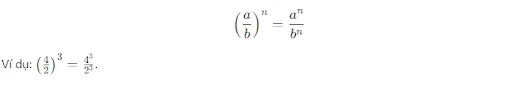
Lũy thừa của số 0 và 1
Lũy thừa với số mũ 0
Bất kỳ số nào khác 0 khi nâng lên lũy thừa 0 đều bằng 1. Công thức tổng quát:
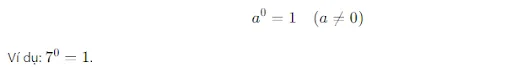
Lũy thừa với số mũ âm
Khi số mũ là số âm, lũy thừa sẽ tương đương với nghịch đảo của số đó với số mũ dương. Công thức tổng quát:
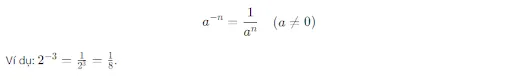
Ứng dụng của quy tắc lũy thừa
Quy tắc lũy thừa không chỉ là một phần quan trọng trong toán học cơ bản mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, từ khoa học, kỹ thuật đến kinh tế và công nghệ thông tin. Dưới đây là những ứng dụng chi tiết của quy tắc lũy thừa trong các lĩnh vực khác nhau.
Ứng dụng trong toán học và giải phương trình
Quy tắc lũy thừa là công cụ cơ bản để giải các phương trình chứa lũy thừa. Nhờ quy tắc lũy thừa, ta có thể đơn giản hóa và rút gọn các phương trình phức tạp, đặc biệt là các phương trình mũ, logarit và đa thức. Ví dụ, khi gặp phương trình như 2^(x+3) = 2^5 , ta có thể áp dụng quy tắc so sánh các số mũ để tìm ra giá trị của x.
Ngoài ra, quy tắc lũy thừa cũng giúp xác định nghiệm của các phương trình bậc cao bằng cách tách thành những thành phần nhỏ hơn và dễ giải quyết hơn.
Ứng dụng trong khoa học và kỹ thuật
Trong các lĩnh vực khoa học như vật lý, hóa học, và thiên văn học, quy tắc lũy thừa được sử dụng để biểu diễn và tính toán các đại lượng lớn hoặc nhỏ. Ví dụ:
- Trong vật lý, công thức tính năng lượng hoặc sức mạnh của một nguồn bức xạ thường được biểu diễn dưới dạng lũy thừa, như công thức tính công suất của sóng âm hoặc sóng điện từ.
- Trong hóa học, quy tắc lũy thừa được áp dụng khi tính toán số lượng phân tử hoặc nguyên tử trong các phản ứng hóa học, đặc biệt là khi liên quan đến các đại lượng rất lớn hoặc rất nhỏ (như số Avogadro).
Ứng dụng trong kinh tế và tài chính
Quy tắc lũy thừa được áp dụng trong các công thức tài chính liên quan đến lãi suất kép, đầu tư, và tăng trưởng kinh tế. Ví dụ:
- Công thức tính lãi suất kép sử dụng quy tắc lũy thừa để tính giá trị tương lai của một khoản đầu tư sau một khoảng thời gian nhất định. Đây là công cụ quan trọng để các nhà đầu tư và ngân hàng tính toán lợi nhuận của các khoản vay và đầu tư dài hạn.
- Trong các mô hình kinh tế, quy tắc lũy thừa còn giúp mô tả tốc độ tăng trưởng theo thời gian, ví dụ như tăng trưởng dân số, tăng trưởng GDP, hay lạm phát.
Ứng dụng trong công nghệ thông tin và khoa học máy tính
Quy tắc lũy thừa cũng rất phổ biến trong lĩnh vực công nghệ thông tin và khoa học máy tính. Ví dụ:
- Trong lập trình và thuật toán, các phép toán lũy thừa được sử dụng để tính toán và tối ưu hóa hiệu suất của các chương trình. Một ví dụ cụ thể là thuật toán sắp xếp và tìm kiếm, nơi việc sử dụng lũy thừa có thể giúp xác định độ phức tạp của thuật toán .
- Trong lý thuyết thông tin và mã hóa, quy tắc lũy thừa giúp tạo ra các mã bảo mật phức tạp. Các phương pháp mã hóa như RSA sử dụng lũy thừa và các quy tắc liên quan để mã hóa và giải mã thông tin, đảm bảo an toàn dữ liệu.
Ứng dụng trong khoa học tự nhiên và sinh học
Trong sinh học, quy tắc lũy thừa được áp dụng để mô hình hóa các hiện tượng tăng trưởng và phân chia tế bào. Ví dụ:
- Mô hình tăng trưởng của vi khuẩn thường sử dụng lũy thừa để dự đoán sự gia tăng dân số của vi khuẩn trong một môi trường nhất định sau một khoảng thời gian. Nếu một loại vi khuẩn phân chia sau mỗi giờ, số lượng vi khuẩn có thể được biểu diễn dưới dạng 2^n, với n là số giờ.
- Trong di truyền học, quy tắc lũy thừa được áp dụng khi phân tích sự di truyền các đặc điểm di truyền qua các thế hệ, đặc biệt khi tính toán khả năng kết hợp các gen và tỉ lệ xuất hiện của các tính trạng.
Ứng dụng trong kỹ thuật điện và điện tử
Trong kỹ thuật điện và điện tử, quy tắc lũy thừa giúp tính toán công suất, điện áp, và dòng điện trong các mạch phức tạp. Ví dụ:
- Công thức tính công suất trong mạch điện , trong đó V là điện áp và R là điện trở, sử dụng quy tắc lũy thừa để xác định giá trị công suất.
- Trong thiết kế vi mạch, các kỹ sư điện tử sử dụng lũy thừa để tính toán khả năng hoạt động của các linh kiện nhỏ như transistor hoặc mạch vi xử lý, giúp tối ưu hóa hiệu suất và giảm tiêu thụ năng lượng.
Lưu ý gì khi sử dụng quy tắc lũy thừa
Khi áp dụng các quy tắc lũy thừa trong toán học, cần lưu ý một số điểm quan trọng để tránh nhầm lẫn và đảm bảo tính toán chính xác. Các lưu ý này sẽ giúp bạn hiểu rõ hơn về cách sử dụng lũy thừa và tránh những lỗi phổ biến thường gặp.
Kiểm tra cơ số trước khi áp dụng quy tắc
Một trong những lưu ý quan trọng nhất là quy tắc lũy thừa chỉ áp dụng được khi các lũy thừa có cùng cơ số. Nếu cơ số khác nhau, bạn không thể cộng, trừ, hoặc nhân các số mũ với nhau. Ví dụ, với biểu thức , do cơ số khác nhau (3 và 4), bạn không thể cộng số mũ mà phải tính từng lũy thừa riêng biệt.
Xử lý số mũ 0 và số mũ âm cẩn thận
- Số mũ bằng 0: Bất kỳ số nào khác 0 khi nâng lên lũy thừa 0 đều bằng 1. Tuy nhiên, 000^000 không xác định, và bạn cần lưu ý không sử dụng giá trị này trong tính toán vì nó không có nghĩa rõ ràng trong toán học.
- Số mũ âm: Khi gặp số mũ âm, quy tắc lũy thừa cho thấy ta phải lấy nghịch đảo của lũy thừa với số mũ dương tương ứng. Ví dụ, . Điều này có nghĩa là bạn cần biến đổi lũy thừa thành dạng phân số để tiếp tục tính toán.
Chú ý quy tắc khi lũy thừa của một lũy thừa
Khi áp dụng quy tắc lũy thừa của một lũy thừa, cần nhân các số mũ lại với nhau. Tuy nhiên, điều quan trọng là phải thực hiện phép tính theo thứ tự đúng và không cộng số mũ như khi nhân hai lũy thừa cùng cơ số. Ví dụ, .
Lũy thừa của một tích và một thương
- Khi nâng một tích lên lũy thừa, mỗi số trong tích đều phải được nâng lên lũy thừa đó. Ví dụ, . Điều này cũng áp dụng cho phép chia: . Tuy nhiên, cần chú ý rằng không thể áp dụng quy tắc này nếu có sự kết hợp giữa phép cộng hoặc trừ trong biểu thức.
- Đối với các biểu thức có nhiều thành phần phức tạp, hãy đảm bảo bạn tách chúng ra thành từng phần và áp dụng quy tắc đúng để tránh nhầm lẫn.
Cẩn thận với các biểu thức có căn bậc hai và căn bậc ba
Lũy thừa và căn bậc hai hoặc bậc ba có mối quan hệ chặt chẽ với nhau, vì căn bậc hai của một số cũng có thể viết dưới dạng lũy thừa: . Tuy nhiên, khi làm việc với căn, bạn cần chú ý về dấu (âm hoặc dương) của giá trị dưới căn. Ví dụ, khi xử lý , cần hiểu rằng căn bậc hai của số âm không có nghĩa trong tập số thực.
Sử dụng đúng các quy tắc để tránh lỗi phép toán
Khi giải các bài toán hoặc phương trình có lũy thừa, cần luôn kiểm tra lại các quy tắc đã áp dụng để đảm bảo tính chính xác. Đôi khi, những lỗi nhỏ như nhầm lẫn giữa phép cộng và phép nhân số mũ có thể dẫn đến kết quả sai lệch.
Thực hiện tính toán một cách có trình tự
Khi tính toán các biểu thức phức tạp, hãy luôn thực hiện từng bước một, đặc biệt là khi có nhiều lũy thừa khác nhau hoặc khi kết hợp lũy thừa với các phép toán khác (như nhân, chia, cộng, và trừ). Nếu không, bạn có thể dễ dàng bỏ qua hoặc nhầm lẫn giữa các bước, dẫn đến sai sót.
Lưu ý về dấu của cơ số
Khi cơ số là một số âm, dấu của kết quả sẽ phụ thuộc vào số mũ:
- Nếu số mũ là số chẵn, kết quả sẽ là số dương. Ví dụ:
- Nếu số mũ là số lẻ, kết quả sẽ là số âm. Ví dụ:
Điều này rất quan trọng khi giải phương trình hoặc đơn giản hóa các biểu thức có chứa số âm.
Hiểu rõ ý nghĩa và giới hạn của quy tắc lũy thừa
Quy tắc lũy thừa chỉ áp dụng trong những điều kiện nhất định và cần tuân thủ các điều kiện đó. Ví dụ, các quy tắc này không áp dụng được khi cơ số là 0 và số mũ là số âm, vì không có nghĩa trong toán học. Do đó, bạn cần chú ý không áp dụng quy tắc này khi gặp những trường hợp ngoại lệ như vậy.
Xem xét việc sử dụng máy tính
Khi làm việc với các lũy thừa lớn, máy tính có thể là công cụ hữu ích để kiểm tra lại kết quả. Tuy nhiên, bạn nên biết cách thực hiện các phép toán thủ công để hiểu rõ quy trình và không phụ thuộc hoàn toàn vào máy móc, giúp phát hiện và sửa lỗi khi cần thiết.
Nắm vững quy tắc lũy thừa sẽ giúp bạn giải quyết các bài toán số mũ một cách dễ dàng và hiệu quả hơn. Hãy thực hành thường xuyên để áp dụng thành thạo những quy tắc này vào học tập và cuộc sống hàng ngày!